>
Application bijective
Cours gratuits > Forum > Forum maths || En basApplication bijective
Message de asmamoussaoui posté le 26-05-2022 à 02:52:36 (S | E | F)
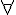x1, x
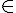ij ; x1=x2
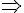f(x1)=f(x2)
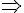{f(2x1-1)= f(2x2-1)
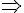2x1-1=2x2-1
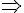x1=x2
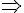y= 2x-1
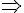x=(y+1)/2
Message de asmamoussaoui posté le 26-05-2022 à 02:52:36 (S | E | F)
Bonjour ! pouvez-vous me corriger l'exercice suivant et me rajouter ce qu'il manque ? merci d'avance !
Soit f une bijection de l’intervalle [-1,3] sur l’intervalle [-1,1] et soit g l’application définie par g (x) = f (2x – 1) .
Montrer que g est une bijection d’un intervalle I sur un intervalle J. Que l’on précisera.
g(x) est une application bijective g surjective et injective
g(x1) = f(2x1-1)
g(x2) = f(2x2-1)
alors c'est une application réciproque
on a : x
I g(x)=f(y)
g(x)=f(2x-1)=f(y)
alors c'est une application surjective
donc, g(x) est une application bijective
Réponse : Application bijective de tiruxa, postée le 26-05-2022 à 18:59:31 (S | E)
Bonjour
La première des choses est de trouver l'intervalle I
Soit l'ensemble des réels x tels que 2x-1 soit compris entre -1 et 3
On trouve rapidement que I=[0;2]
Personnellement j'écrirai que g=fou avec u définie de [0;2] sur [-1;3] par u(x)=2x-1.
Il suffit alors de démontrer que u est une bijection pour pouvoir conclure.
Ceci dit pour la rédaction
injection
Soit x1 et x2 dans I tels que g(x1)=g(x2)
g(x1) = f(2x1-1)
g(x2) = f(2x2-1)
donc
{f(2x1-1)= f(2x2-1)
comme f est injective, on a
2x1-1=2x2-1
donc x1=x2
donc g est injective
et pour la surjection :
Soit y dans [-1,1] cherchons x dans I tel que g(x)=y ou f(2x-1)=y
Comme f est bijective on sait qu'il existe z dans [-1,3] tel que f(z)=y
donc f(2x-1)=f(z)
or f est injective donc
2x-1=z
et x = (z+1)/2
comme z est dans [-1,3] on a bien x dans [0,2]
donc g est surjective
Réponse : Application bijective de hicham15, postée le 26-05-2022 à 19:54:35 (S | E)
Bonjour,
Je veux juste ajouter qq chose qui peut etre utile pour celui qui a posé la question.
On peut juste montrer l'existence et l'unicité de ce x (en surjectivité) pour conclure que c'est une application bijective.
C'est le cas, puisque z existe et c'est unique, puisque f est bijective et x = (z+1)/2.
Cours gratuits > Forum > Forum maths
